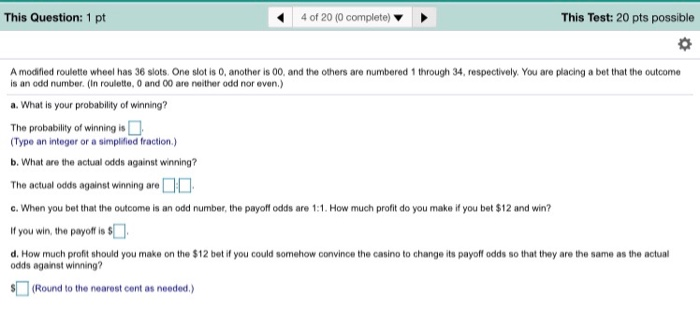
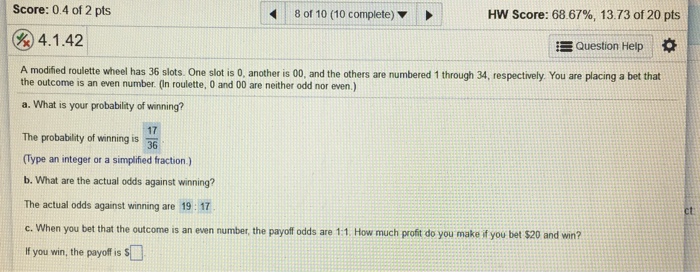
A Modified Roulette Wheel Has 36 Slots
A modified roulette wheel has 44 slots. One slot is 0, another is 00, and the others are numbered 1 through 42, respectively. You are placing a bet that the outcome is an odd number.
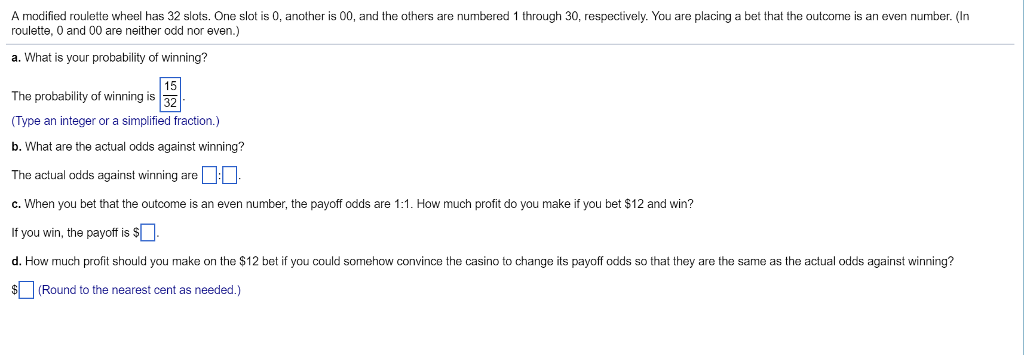
A modified roulette wheel has 28 slots. One slot is 0, another is 00, and the others are number 1 through 26, respectively. You are placing a bet that the outcome is an even number. A modified roulette wheel has 40 slots. One slot is 0, another is 00, and the others are numbered 1 through 38, respectively. You are placing a bet that t. The casino game that bears a similar name to the show is also often referred to as the Big 6 Wheel and is spun vertically (as in Shopper's Bazaar) and also has money on it, except the money used are dollar bills ($1, $2, $5, $10, and $20); and like Roulette, players must bet on which bill they think the wheel will stop on by placing chips on. There are four destination casino resorts in upstate New York. These casinos all offer: blackjack, roulette, craps, slots and video poker. Some casinos also offer: mini-baccarat, poker, pai gow poker, Caribbean stud poker, let it ride, big 6 wheel, bingo, keno, Mississippi stud, three card poker, four card poker and Spanish 21.
6 meters
step-by-step explanation:
your exact question is kind of difficult to understand, so maybe an example will explain what you're supposed to do? i'll work through the first problem on the worksheet.
suppose you have a tray of 652 brownies, and you have 5 friends that you want to feed without picking favorites. how many brownies can you dole out to each of your friends in equal amounts? how many will be left over for you to eat?
what you're doing here is finding a way to arrange the number 652 as the sum of integer multiple of 5 and some remainder:
here ('q' for quotient) is the number of brownies each of your friends get, and is the remainder. that's the basic idea behind division.
we break up the number 652 into parts so that the leading digit stands on its own:
652 = 600 + 52

first we check if it's possible to hand out exactly 100 brownies to each friend. with 5 friends, this means we want to know if we can take out 500 brownies from the tray. we can do this 1 time because we have 600 brownies to take from, and when we do that we're left with 100 + 52 brownies to divvy up. so we know that
652 = 1*500 + 152
next we want to know if it's possible to hand out exactly 10 brownies per friend. if we can, we have to remove 50 brownies from the tray each time until we can't. we have 152 brownies left, and we know that 3(50) = 150, so
152 = 3*50 + 2
now we have 2 brownies left in the tray. is it possible to hand 1 out to each of your 5 friends? no, you'd need a minimum of 5 brownies to do that. so the last 2 are yours.
putting everything together, we found that
652 = 1*500 + 3*50 + 2
and we can rearrange this to write
652 = 5*100 + 5*30 + 2
652 = 5(100 + 30) + 2
652 = 5*130 + 2
so and .
you might be more accustomed to the table depicting the algorithm. that's just a compact way of organizing what we've done above. you can consult the image i've attached below.

where is the graph
step-by-step explanation:
A Modified Roulette Wheel Has 32 Slots
|